MATH

    Before I go into how math, not just simple elementary math, but geometry, algebra, calculus, and  trigonometry was all founded by the Kemetites, I would like to point out that there should lbe little question as to the validity of this claim. It is obvious, for right in the heart of both Nubia, which mothered Kmt, and Kmt itself, lies the very structures that bear witness to the birth, endowment, cultivation, and science of the universal language, mathmatics. For in Kush and Kmt are the geometrical structures known as pyramids. Is not a pyramid a geometrical structure? Would'nt an ancient nation even as advanced as the Kushites and the Kemetites need geometrical, trigonometrical, and scientific formulas and knowledge to even build these structures? Of course:

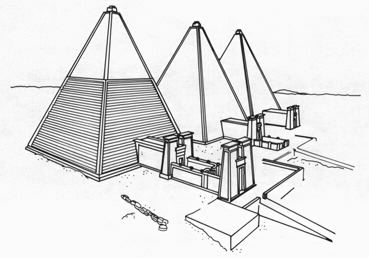
(The Kushite Pyramids)                                                                    (The Kemetite Pyramids)

    It seems very evident to all historians that are not influenced by the stubborn more Euro side of history that one needs not even to ponder on whether or not the Egyptians, as well as the Nubians , knew complexed forms of scientifc mathematics. Evidence shows that the cultivation of geometry, trigonometry and calculas apexed during the time of the construction of the Great Pyramids in Egypt (Papyrus of Moscow and the Rhine Papyrus); something that would be imparative to the construction and design of the Pyramids.  From this evidence alone, one would automatically draw the inference that geometry, algebra and trignometry were needed as well as used to blueprint, prototype, and build the pyramids of Africa. But, due to the stubborness and convicted hearts of the Euro-historians, whose core belief is that no such African mathematics could predate, nor give birth, to European mathmatics, allows the debate to go on within their circles; a debate long settled in the scholarly circles of Afro and Asiatic historical debates and works. Even with the obvious and conspicuous ancient evidence (The papyrus of Rhine and Moscow), both of the Kemetites and the ancient Greeks bearing witness in letteres, historical accounts and scholarly texts, the Euro-historians turn a blind eye and a deaf ear. I have always felt that this has happened because if they acknowledge it as true, they will then have to acknowledge that Thales, Pathagorus, and Archimedes all took the secret knowledge from African priests, or Egyptians and used it to gain noteriety amoung the Greco-European world, thus becoming plagiarists.

    Moreover, it would also be evident that if the Euro-historical community acknowledged that Kemet originated the science of mathmatics all other attachments to this fact would then be known as true. For example, if the Greeks such as Thales and Pythagorus did study in Kemet by the priest in mystery schools, which the Afro-historical community know to be true, then it can easily be known that the knowledge of masonry was then derived and based on the speculative wisdom of the Egyptians.

    Race is also a consideration. One must realize that in the historical community Greece and Rome has been so vastly studied and researched that it has been so puffed up to  look as if it was the originator of all science, medicine, religion,  ect... If the hisorical establishment (Euro-historical) acknowledged that Kemet did originate these sciences, then all that has been taught, in the Euro-historical community, about Greco science, as it relates to origination,  would be shown to be a falacy; thus redifinng how history is taught in schools and colleges. Colleges would no longer give praise to the achievements of Pathagorus, but Egyptian priests, who were blackmen as opposed to the white Greek.

To show you that the Ancient Egyptians did originate the science of mathmatics lets use some evidence:
 
 

Geometry:

    Archimedes, the so-called father of geometry, was noted for supposedly discovering a sphere inscribed in a right cylinder of a height equal to the diameter of the sphere (This was his epitaph). For this to have happened, Archimedes had to know, invent, or find the formula of the area of the right cylinder. Also, for the sphere to be tangent to the rt. cylinder, he would have to  know, invent, or find the formula of the area of a sphere so that the sphere's  diameter would be equal in hieght to the rt. cylinder. Moreover, the formula of the volumes of both the cylinder and the sphere had to be known as well.  This was considered Archimedes greatest "invention," but little did he know that the Egyptians who taught him his "invention," kept papyrus scrolls which lasted thousands of years, and was discovered by archaeologists.  V.V. Struve, an egyptian scholar, published the Papyrus of Moscow in 1930 to the international scientific community.
 

Note: I could not find a symbol for pi, so I had to improvise, please excuse the god. The symbol for pi in this case is : ¶

The scroll shows the formula for the area of a sphere ( S=4¶R² ). Again let me remind you that  this dates back to 2000 B.C.  In addition to the Papyrus of Moscow, archaeologist discovered the  Rhine Papyrus which was published by T. Eric Peet. The Rhine Papyrus shows us the calculations of a cylinder and gives us the volume of a cylinder ( V= ¶R² ) and the constant ratio of the area of a circle (sphere) and its diameter, something that would have to be known in order to do what Archimedes did. The Rhine Papyrus was dated back to 1800 B.C., almost two millenia before Archimedes.  The fact that this was found, gives us all the more reason to infer that the Egyptians knew the area of cylinder as well. We can say this because they knew the volume of a cylinder, a shape that when cut in right places would become a rectangle, something to which they already knew how to calculate the area to. Moreover, they had to know the area of the cylinder, because one cannot consturct a cylinder without first knowing the area of a sphere or circle, something to which the Egyptians already knew. We know this because of the Papyrus of Moscow. Thus, it is known that both these papyrus scrolls gave all the formulas necessary to construct the same geometric structures before that of Archimedes, who took line by line these formulas when studying in the Egyptian mystery schools. Archimedes studied in Egypt for decades, thus learning all the "mysteries," including the mystery of mathmatics.
 
 

(incidently these trunicated pyramids are located in Kush(Nubia), which alone attests to the close relationship of Egypt and Nubia as two black allies.  This is why the bible refers to both in its prophesys interchangeably:
 

  Moreover, the scientific community puts the pyramids of Kush very late in  the game, around 1200 to 600 B.C., something to which, I theorize, to be a miscalculation.  My theory is that Nubian,( Kushite) civilization preceeded that of Egypt, thus giving knowledge that was evident in the conception of Kush, in the sciences, to that of Egyptian (Kemetite) civilization. This is why the trunicated pyramid, something to which can only be found in Nubia, was found in the Papyrus of Moscow around 2000 B.C. There is alot of other evidence that I could go into, but for the sake of time, I will no mention. But there is one piece of evidence I have to include, in the  excavations by Keith Seele, at the Qostul cemetery, a censer was found. On the censer was remains of a king sitting in a royal boat wearing the long white crown of Upper Egypt ( to us, the southern most part of Egypt and parts of Nubia). Also one could see the design of a temple palace behind the boat, this design is found at the funeral domain of Pharoah Zoser at Saqqara (2778 B.C.), the pharoah of the first Egyptian pyramid, the step pyramids which are also found in Kush.  Above the white crown is the Falcon-god Horus, smybolic of royalty. The censer is the most ancient figure of a king found in the Nile Valley, giving evidence that the crown of Upper Egypt, thought to be associated only  with Egyptian monarchy, possessed the evidence that the monarchy of Kush preceeded that of Egypt. This censer was found in a tomb, which was a pyramid, also giving evidence that Kushite pyramids preceeded that of Kemet's (Egypt's).
 

    The Papyrus of Moscow dates back to 2000 B.C., a time nearly two thousand years before the birth of Archimedes. The fact that this payrus was not a piece of scratch paper with the scribbling on of trial and error type formulas, yet was a book kept by the scribes as formulas in which to aquire knowledge from, gives supporting evidence that geometry was in use well before the creation of this scroll (2000 B.C.). Also, the making of the pyramids alone gives evidence to the fact that geometry was invented, prototyped and in use during the time of the pyramid constructions (2700 to 2400 B.C), because one cannot derive the formula for the area, perimeter, or volume of a triangle unless one already had the formulas of the cylinder, cone, and sphere. Hence,it is my belief that the pyramid was born out of the spehere and cylinder. The reason for this, is because the lengths would be already established through the discovery of the formulas of cylinders, cones and spheres.

    In excercise 14 of the Papyrus of Moscow dealing with the calculation of the volume of the trunicated pyramid tells us that the Egyptians, once again, outdated that of Archimedes, who says that his friend Eudoxus, who studied in Egypt for decades as well, found the measurement of the pyramid and the cone. This is a huge farse. What better people to know the how to design, calculate and scientifically theorize on the pyramid than the ancient Kemetites and the Kushites, who are the only people in antiquity to construct mass structures of these designs as burial tombs: ???? Hmmmmmmm. You tell me. So then, how can the measurement of the pyramid and cone, a geometrical structure which was most likely materialized before the pyramid, be attributed to Eudoxus, who studied in Kemet for decades, and lived 3000 to 2500 years after the pyramids, the very geometrical structure he claimed he founded the measurement of, were erected???Hmmmm. Sounds like someone has been caught in a hoax, an activity characteristic of the euro-historical institutions (the destroying of Kemetic scrolls and art, i.e. Napoleon, the chisling of the nose of the Sphinx, the omission of African American historic achievement in the U.S, etc...) Moreover the  Rhind Papyrus (exercises 37,38,39,40) and the Papyrus of Moscow (exercises 56,57,58,59, and 60) show us the that the priests of Kemet derived and studied the mathematics of the pyramid and the cone, thousands of years before the Greeks. Moreover, these scrolls shows us that they even used different trigonometric linnes such as the tangent, the sine, the cosine, and the contangent  so that one could calculate slopes, and waht better structure to calculate slopes for than a pyramid?
 

"Furthermore, Eudoxus and Plato were former pupils of the Egyptian priests at Heliopolis, but as the documents prove, the Egyptians had already preceeded, two thousands years before the birth of these two, with the study that is attributed to them. In fact the cube, the pyramid, etc., are also a part of the basic volumes improperly "baptized" Plutonic bodies of work."
("Civilization or Barbarism: An Authentic Anthropology" Dr. Cheikh Anta Diop, pg 237)

Papyrus of Moscow:
(notice ther trunicated pyramid)

Rhine Papyrus:

"Archimedes chose as his epitaph, considering that this is his best discovery. Thus, Archimedes did not even have the excuse of an honest scholar who would rediscover an established theorem, without knowing that it had been discovered two thousand years before him by his Egyptian predecessors. The other "borrowings" in which he indulged himself during and after his trip to Egypt, without ever citing the sources of his inspiration, show clearly that he was perfectly conscious of his sin, and that hereby he was being faithful to the Greek tradition of plagarism that went back to Thales, Pythagorus, Plato, Eudoxus, Oenopides, Aristotle, ect., which the testimonies of Herodotus and Diodorus of Sicily reveal to us in part." (Diop, 242)

Note:  If Archimedes invented this screw while in Egypt, then why does Diodorus call the screws Egyptian as opposes Archimedian of Greek??? Because they were used before that of Archimedes.

Click here to continue

Go Home    hit my box